Stellated Polyhedra

This material is suitable for children of any school age.

Understanding of geometric shapes and forms is achieved through the class’s project work. Every object in our world has its shape, structure, composition, and texture. Each body is beautiful in its own right. The project work is related to the topic of “Stellated Polyhedra”.

A stellated polyhedron is a regular non-convex polyhedron whose faces intersect each other. The forms of stellated polyhedra are used in decorative art and architecture. The first stellated polyhedra were discovered by J. Kepler, and 200 years later, they were constructed by the mathematician and mechanic L. Poinsot. That is why stellated polyhedra are called Kepler-Poinsot solids.

In the lesson, we will construct stellated polyhedra from paper and cardboard. Students will work in groups, helping each other with the modeling. The visually impaired student should sit at the first desk of the middle row. It is better to attach a magnifying glass above the desk so the child can perform and see the main aspects of the practical work. The visually impaired student should be involved in the general flow of the lesson and should comment on the constructions being made. The “hand in hand” method can be used, where the teacher helps the visually impaired student to better glue the models.

As a result of extending the edges of a dodecahedron, a polyhedron called the small stellated dodecahedron arises. The teacher and the visually impaired student glue together the dodecahedron model, using a ready-made template. The template can be found on the internet.

Drawing 1. Dodecahedron model.

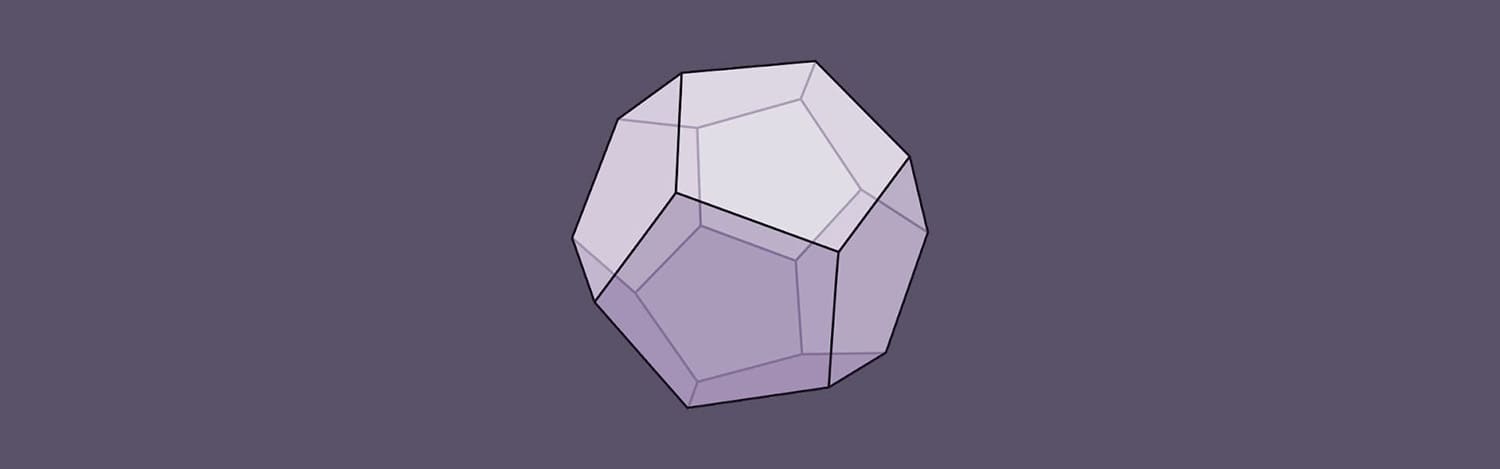
Constructing geometric figures is one of the fundamental skills that foster the formation of spatial representations of the surrounding world. Also, no one in the world can do without spatial representations of objects.

The group of kids who worked on the dodecahedron answers questions:

• How many faces does a dodecahedron have?
• What polygons are the faces of the dodecahedron?
• How many vertices?
• In Plato’s idealistic worldview, he called the dodecahedron the model of the Universe. Why did Plato call the dodecahedron specifically the model of the Universe?

The answers to these questions can be very diverse.

Another group of students, using polyhedron templates, model the small stellated polyhedron. The class can be divided into several groups to have more interesting models, and everyone can work on a project. The group of kids with poor vision work under the guidance and with the help of the teacher.

Drawing 2. Polyhedron model.

The beauty of the polyhedron. The amazing world of geometric bodies, possessing unique properties.

Question: Where can such polyhedra be applied?

Answer: Jewelry, architecture, snowflakes.