Rectangular Parallelepiped
The challenge of developing spatial understanding is closely linked to the principle of visualization and tactile experience. What should those who lack visual aids do? The answer lies in replacing visual cues with tactile ones and teaching children to mentally construct geometric figures.
Visually impaired children typically have a limited repertoire of spatial concepts compared to their sighted peers. It’s crucial for educators to enrich this repertoire, gradually teaching them to recreate mental images of geometric shapes.
Let’s consider the topic of “Rectangular Parallelepiped” as an example.
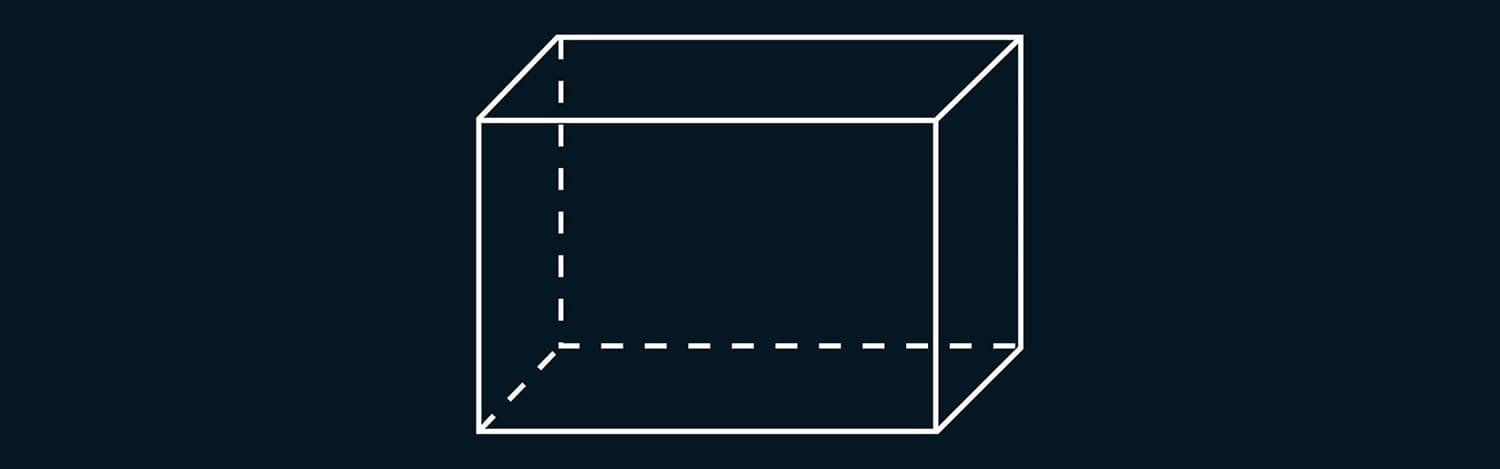
Introductory concepts about polyhedra are typically covered in high school. To study the topic of a rectangular parallelepiped, it’s advisable to use assembled models, so the student can visually identify the main elements of the polyhedron. Each student should work with a tangible model. Only in this way can we say that a visually impaired student forms a correct understanding of the spatial figure.
Questions about the rectangular parallelepiped:
- How many faces does the parallelepiped have?
- How many edges?
- How many vertices?
- What familiar objects are shaped like a rectangular parallelepiped?
- What are the dimensions of a rectangular parallelepiped?
Students might recall that a book and a matchbox are shaped like a rectangular parallelepiped, as well as a room and a house.
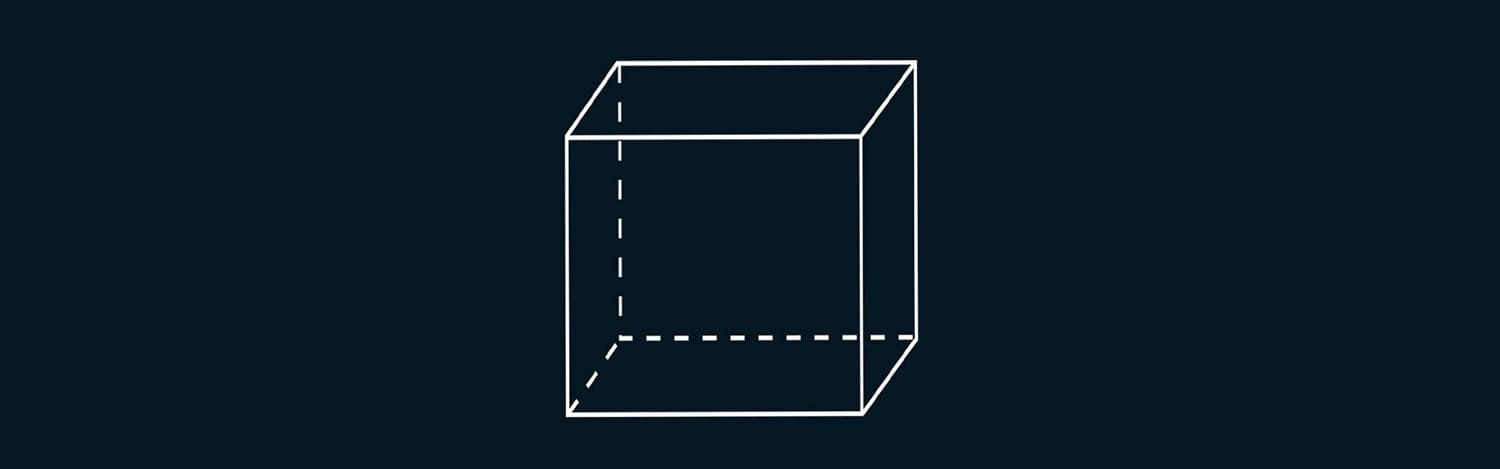
Suggest comparing a cube model with a rectangular parallelepiped model. What are the differences? What are the similarities? When examining the models, students should note that a cube has all edges equal.
Discuss with the students what the sum of the edges’ lengths of a rectangular parallelepiped is. How many equal edges does a rectangular parallelepiped have? What formula for the sum of the edges’ lengths can be derived? Using the parallelepiped model, students derive the formula.
What formula would be used for the sum of the lengths of the edges of a cube? Where in everyday life might the sum of the lengths of edges be useful? One answer involves a piece of wire from which a model of a rectangular parallelepiped can be made. There are also responses related to electrical wiring in a house. To accurately calculate the required amount of cable, one must calculate the sum of the lengths of edges within an apartment.
We also need to derive the formula for the surface area of a rectangular parallelepiped.
Continuing to work with the model of the rectangular parallelepiped and the cube, how many faces does the rectangular parallelepiped have? What kind of polygon is this?
To answer these questions, one might prepare rectangles with embossed lines along the edges so that a child with impaired vision can more easily transition from thinking about a volumetric body to a polygon.

We recall how to find the area of a rectangle. Students count the equal faces of the rectangular parallelepiped and derive the formula. The teacher must write clearly and legibly on the board, explaining what is written in an understandable way. We then discuss the surface area of a cube. How does the formula for the surface area of a cube differ from that of the parallelepiped?
Where in life might knowing these formulas be useful? Many say it’s useful for home renovations.
The teacher’s task is to engage the student in the subject, showing them that they can solve any problems.
