Broken Line and Polygon
This material is suitable for children of any school age.
These developments are suitable for those who teach or want to teach a visually impaired child mathematics.
How to help a visually impaired child love mathematics if their ability to visually examine objects is limited? I will answer this question as follows: it is possible, necessary, and vitally important. Why is it possible? We replace visualization with touch and hearing. Why is it necessary and vitally important? The child needs to feel the power and beauty of mathematical thinking. Mathematics surrounds us in reality. It is not for nothing that mathematics is called the queen of sciences. This science links almost all subjects together, including chemistry and physics, literature and biology, and others.
Today, in the lesson, we are examining the concept of a “broken line”. The teaching material for the lesson is counting sticks. Let’s make the number “zero” out of four sticks. We get a closed broken line. Now, let’s make the number “nine” out of 5 sticks. We get an open broken line.
Question: What is a broken line?
Answer: A broken line is a sequence of points connected by line segments. Students come up with a definition based on the constructions of numbers. It can be said that a broken line comes from the word “break”. If you break a stick, you get a broken line.
Question: What geometric figures make up a broken line?
Answer: It consists of line segments. These segments are called links, and the points of inflection of the broken line are its vertices.
Question: Where can you encounter a broken line in life?
Answer: Students who have already constructed diagrams recall that there the points of the graph are connected by line segments. A broken line is found in action signs, such as “greater than” or “less than”, as well as in the signs “plus” and “minus”.
Let’s draw an open broken line ABCD on the board and measure its length.
Figure 1. Open broken line ABCD
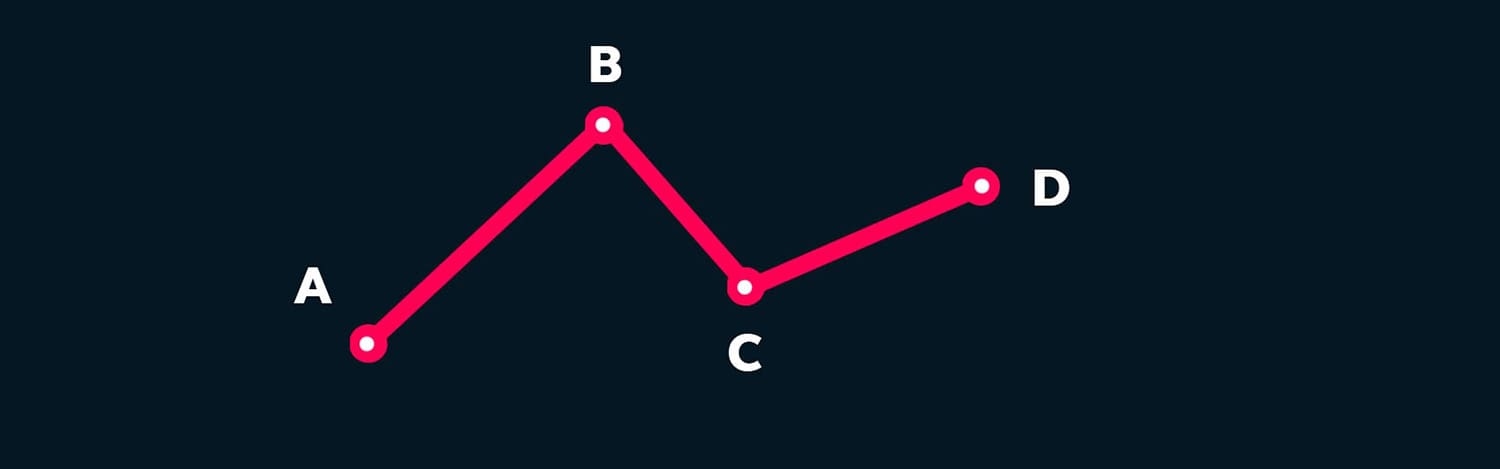
To measure the length of a broken line, it is necessary to measure its segments. For visually impaired students, there are modified rulers with grooves cut into them for easy orientation by touch along the scale of divisions.
To facilitate understanding for visually impaired students, we lay out the open broken line ABCD on the desk. We measure the segments and find the length of the entire broken line. For constructing the broken line, counting sticks of different lengths can be used.
By assembling counting sticks into a triangle, we get a closed broken line. A polygon can also be formed by assembling a pentagon, defining a polygon as a closed broken line where the vertices are called the vertices of the polygon, and the segments are the sides.
Question: What is the perimeter of a polygon?
At the end of the lesson, we can look at a star map.
Figure 2. Star map
There are constellations that form broken lines, for example, the constellation Cassiopeia.
The lesson should include a change in activity types. It is advisable to offer students to perceive text and tasks by ear every 5-10 minutes of visual work. This not only gives rest to the eyes but also develops auditory perception. It should be remembered that the speed of task completion for children with visual impairments is 70% lower than that of healthy children. In my lessons, I constantly change the types of activities so that children do not get tired and find it interesting.