Mutual arrangement of lines in space
For geometry lessons with a visually impaired student, it’s useful to use models of geometric solids, and discuss the shapes of the most common real-world objects and items instead of drawings on the board.
Visually impaired students often find it challenging to construct geometric figures and work with ready-made drawings. In this case, construction activities can be helpful.
To facilitate the perception of educational material, it’s recommended to place the student at the front desk of the middle row and install a magnifying glass above the desk so that they can see the main points of practical work.
To study the theme of lines in space, pencils can be used to create a triangular pyramid. For this, take 6 pencils and join their ends with tape to form a pyramid.
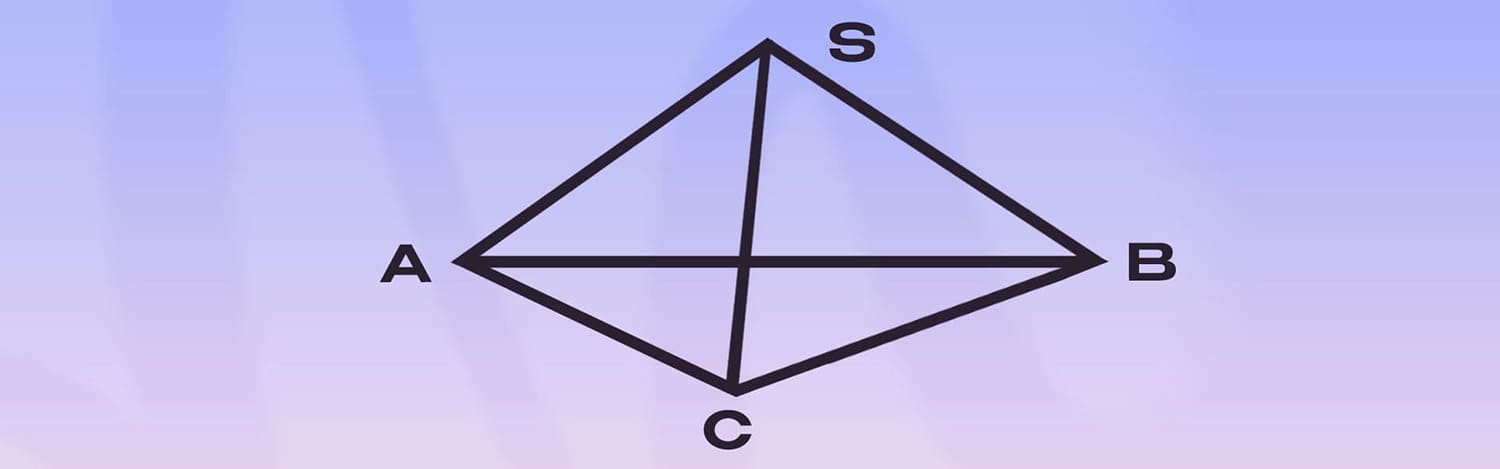
If the pencils are equal in length, a tetrahedron will be formed.
Now, the pyramid model can be used to discuss intersecting and skew lines. For example, lines AC and BC intersect, lie in the same plane, and have one point of intersection.
The visually impaired student works with the pyramid model and then will perform the drawing under the teacher’s guidance.
Consider lines AS and BC. What kind of lines are these? These lines are called skew lines because they do not lie in the same plane. It’s important to engage the visually impaired student in the general course of the lesson so that they can comment on the drawings being made. For this, working with the model is necessary. On the board, you can draw a pyramid, marking intersecting and skew lines.
Where in life can you find skew lines? For example, subway lines and roads. Many transport interchanges are made in the form of skew lines.

Continuing to work with the pyramid model, you can discuss which other lines will be skewed and intersecting. You can also consider the classroom and give examples of skew and intersecting lines.
Thus, the visually impaired student learns to navigate in the simplest geometric situations and develops the ability to describe the results of the work.
Let’s consider another model or layout with parallel lines. Let’s take the familiar rectangular parallelepiped. Draw the figure on the board. The prism model can be made of soft wire. This model is better prepared in advance.

In a rectangular parallelepiped, students can find parallel lines. They conclude about the parallelism of the lines because they are in the same plane and do not intersect. For the visually impaired student, the teacher guides the child’s hand when examining the figure and its elements. You can ask, “Will lines always be parallel if they have no common points?” The answer is, “No, they can be skewed.”
Using the model of a rectangular prism, you can record skew lines, parallel lines, and intersecting lines.
